二分查找底层依赖的是数组随机访问的特性,所以只能用数组来实现。如果数据存储在链表中,就真的没法用二分查找算法了吗?
实际上,我们只需要对链表稍加改造,就可以支持类似“二分”的查找算法。我们把改造之后的数据结构叫作跳表(Skip list),也就是今天要讲的内容。
跳表这种数据结构对你来说,可能会比较陌生,因为一般的数据结构和算法书籍里都不怎么会讲,跳表这个数据结构出现的时间相对与其他数据结构出现的较晚,大概在1980年左右才出现,所以大多数的系统底层都是使用树等其他数据结构实现的。但是它确实是一种各方面性能都比较优秀的动态数据结构,可以支持快速的插入、删除、查找操作,写起来也不复杂,甚至可以替代红黑树(Red-black tree)。
Redis 中的有序集合(Sorted Set)就是用跳表来实现的。如果你有一定基础,应该知道红黑树也可以实现快速的插入、删除和查找操作。那 Redis 为什么会选择用跳表来实现有序集合呢?
如何理解“跳表”?
对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。
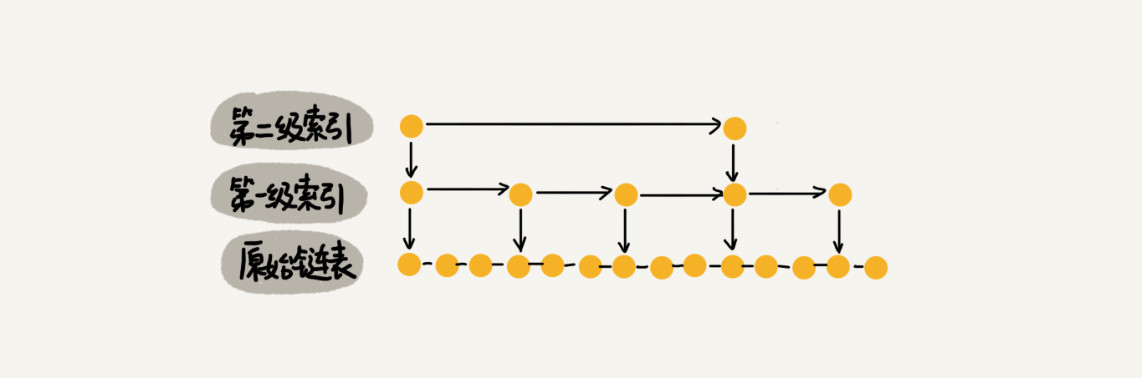
那怎么来提高查找效率呢?如果像图中那样,对链表建立一级“索引”,查找起来是不是就会更快一些呢?每两个结点提取一个结点到上一级,我们把抽出来的那一级叫作索引或索引层。你可以看我画的图。图中的 down 表示 down 指针,指向下一级结点。
如果我们现在要查找某个结点,比如 16。我们可以先在索引层遍历,当遍历到索引层中值为 13 的结点时,我们发现下一个结点是 17,那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针,下降到原始链表这一层,继续遍历。
这个时候,我们只需要再遍历 2 个结点,就可以找到值等于 16 的这个结点了。这样,原来如果要查找 16,需要遍历 10 个结点,现在只需要遍历 7 个结点。
从这个例子里,我们看出,加来一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了。那如果我们再加一级索引呢?效率会不会提升更多呢?跟前面建立第一级索引的方式相似,我们在第一级索引的基础之上,每两个结点就抽出一个结点到第二级索引。现在我们再来查找 16,只需要遍历 6 个结点了,需要遍历的结点数量又减少了。
我举的例子数据量不大,所以即便加了两级索引,查找效率的提升也并不明显。为了让你能真切地感受索引提升查询效率。我画了一个包含 64 个结点的链表,按照前面讲的这种思路,建立了五级索引。
从图中我们可以看出,原来没有索引的时候,查找 62 需要遍历 62 个结点,现在只需要遍历 11 个结点,速度是不是提高了很多?
所以,当链表的长度 n 比较大时,比如 1000、10000 的时候,在构建索引之后,查找效率的提升就会非常明显。前面讲的这种链表加多级索引的结构,就是跳表。我通过例子给你展示了跳表是如何减少查询次数的,现在你应该比较清晰地知道,跳表确实是可以提高查询效率的。接下来,我会定量地分析一下,用跳表查询到底有多快。
用跳表查询到底有多快?
前面我讲过,算法的执行效率可以通过时间复杂度来度量,这里依旧可以用。我们知道,在一个单链表中查询某个数据的时间复杂度是 O(n)。那在一个具有多级索引的跳表中,查询某个数据的时间复杂度是多少呢?这个时间复杂度的分析方法比较难想到。
我把问题分解一下,先来看这样一个问题,如果链表里有 n 个结点,会有多少级索引呢?按照我们刚才讲的,每两个结点会抽出一个结点作为上一级索引的结点,那第一级索引的结点个数大约就是 n/2,第二级索引的结点个数大约就是 n/4,第三级索引的结点个数大约就是 n/8,依次类推,也就是说,第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k级索引结点的个数就是 n/(2k)。假设索引有 h 级,最高级的索引有 2 个结点。通过上面的公式,我们可以得到 n/(2h)=2,从而求得 h=log2n-1。
如果包含原始链表这一层,整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候,如果每一层都要遍历 m 个结点,那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。那这个 m 的值是多少呢?按照前面这种索引结构,我们每一级索引都最多只需要遍历 3 个结点,也就是说 m=3,为什么是 3 呢?
我来解释一下。假设我们要查找的数据是 x,在第 k 级索引中,我们遍历到 y 结点之后,发现 x 大于 y,小于后面的结点 z,所以我们通过 y 的 down 指针,从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有 3 个结点(包含 y 和 z),所以,我们在 K-1 级索引中最多只需要遍历 3 个结点,依次类推,每一级索引都最多只需要遍历 3 个结点。
通过上面的分析,我们得到 m=3,所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找,是不是很神奇?
不过,天下没有免费的午餐,这种查询效率的提升,前提是建立了很多级索引,也就是我们在第 6 节讲过的空间换时间的设计思路。
跳表是不是很浪费内存?
比起单纯的单链表,跳表需要存储多级索引,肯定要消耗更多的存储空间。那到底需要消耗多少额外的存储空间呢?我们来分析一下跳表的空间复杂度。跳表的空间复杂度分析并不难,我在前面说了,假设原始链表大小为 n,那第一级索引大约有 n/2 个结点,第二级索引大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下 2 个结点。如果我们把每层索引的结点数写出来,就是一个等比数列。
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。
计算过程
n/2, n/4, .., 2 这个数列中一共有log2(n/2)项
等比数列求和公式
S = a0(1-q^n)/(1-q)
其中a0表示首项,n表示项数
这里的a0=n/2, 项数=log2(n/2), q=1/2,其中由对数的恒等式2log2(X)=X可得s=n(1-2log2(2/n))
S = n/2(1-2/n)/(1-1/2) = n-2
也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。那我们有没有办法降低索引占用的内存空间呢?我们前面都是每两个结点抽一个结点到上级索引,如果我们每三个结点或五个结点,抽一个结点到上级索引,是不是就不用那么多索引结点了呢?我画了一个每三个结点抽一个的示意图,你可以看下。
从图中可以看出,第一级索引需要大约 n/3 个结点,第二级索引需要大约 n/9 个结点。每往上一级,索引结点个数都除以 3。为了方便计算,我们假设最高一级的索引结点个数是 1。我们把每级索引的结点个数都写下来,也是一个等比数列。

通过等比数列求和公式,总的索引结点大约就是 n/3+n/9+n/27+…+9+3+1=n/2。尽管空间复杂度还是 O(n),但比上面的每两个结点抽一个结点的索引构建方法,要减少了一半的索引结点存储空间。
实际上,在软件开发中,我们不必太在意索引占用的额外空间。在讲数据结构和算法时,我们习惯性地把要处理的数据看成整数,但是在实际的软件开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
高效的动态插入和删除
跳表长什么样子我想你应该已经很清楚了,它的查找操作我们刚才也讲过了。
实际上,跳表这个动态数据结构,不仅支持查找操作,还支持动态的插入、删除操作,而且插入、删除操作的时间复杂度也是 O(logn)。
我们现在来看下, 如何在跳表中插入一个数据,以及它是如何做到 O(logn) 的时间复杂度的?我们知道,在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是 O(1)。
但是,这里为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找操作就会比较耗时。对于纯粹的单链表,需要遍历每个结点,来找到插入的位置。但是,对于跳表来说,我们讲过查找某个结点的的时间复杂度是 O(logn),所以这里查找某个数据应该插入的位置,方法也是类似的,时间复杂度也是 O(logn)。我画了一张图,你可以很清晰地看到插入的过程。
好了,我们再来看删除操作。如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。
当然,如果我们用的是双向链表,就不需要考虑这个问题了。
跳表索引动态更新
当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。
作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入、删除操作性能下降。
如果你了解红黑树、AVL 树这样平衡二叉树,你就知道它们是通过左右旋的方式保持左右子树的大小平衡(如果不了解也没关系,我们后面会讲),而跳表是通过随机函数来维护前面提到的“平衡性”。当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。
如何选择加入哪些索引层呢?我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
解答开篇
今天的内容到此就讲完了。现在,我来讲解一下开篇的思考题:为什么 Redis 要用跳表来实现有序集合,而不是红黑树?Redis 中的有序集合是通过跳表来实现的,严格点讲,其实还用到了散列表。
不过散列表我们后面才会讲到,所以我们现在暂且忽略这部分。如果你去查看 Redis 的开发手册,就会发现,Redis 中的有序集合支持的核心操作主要有下面这几个:插入一个数据;删除一个数据;查找一个数据;按照区间查找数据(比如查找值在[100, 356]之间的数据);迭代输出有序序列。
其中,插入、删除、查找以及迭代输出有序序列这几个操作,红黑树也可以完成,时间复杂度跟跳表是一样的。但是,按照区间来查找数据这个操作,红黑树的效率没有跳表高。对于按照区间查找数据这个操作,跳表可以做到 O(logn) 的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历就可以了。这样做非常高效。
当然,Redis 之所以用跳表来实现有序集合,还有其他原因,比如,跳表更容易代码实现。虽然跳表的实现也不简单,但比起红黑树来说还是好懂、好写多了,而简单就意味着可读性好,不容易出错。还有,跳表更加灵活,它可以通过改变索引构建策略,有效平衡执行效率和内存消耗。
不过,跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些,很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候,直接拿来用就可以了,不用费劲自己去实现一个红黑树,但是跳表并没有一个现成的实现,所以在开发中,如果你想使用跳表,必须要自己实现。
内容小结
今天我们讲了跳表这种数据结构。跳表使用空间换时间的设计思路,通过构建多级索引来提高查询的效率,实现了基于链表的“二分查找”。
跳表是一种动态数据结构,支持快速的插入、删除、查找操作,时间复杂度都是 O(logn)。
跳表的空间复杂度是 O(n)。不过,跳表的实现非常灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗。虽然跳表的代码实现并不简单,但是作为一种动态数据结构,比起红黑树来说,实现要简单多了。所以很多时候,我们为了代码的简单、易读,比起红黑树,我们更倾向用跳表。


